2146번: 다리 만들기
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다
www.acmicpc.net
문제
여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.
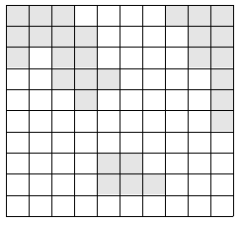
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.

물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).
지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.
입력
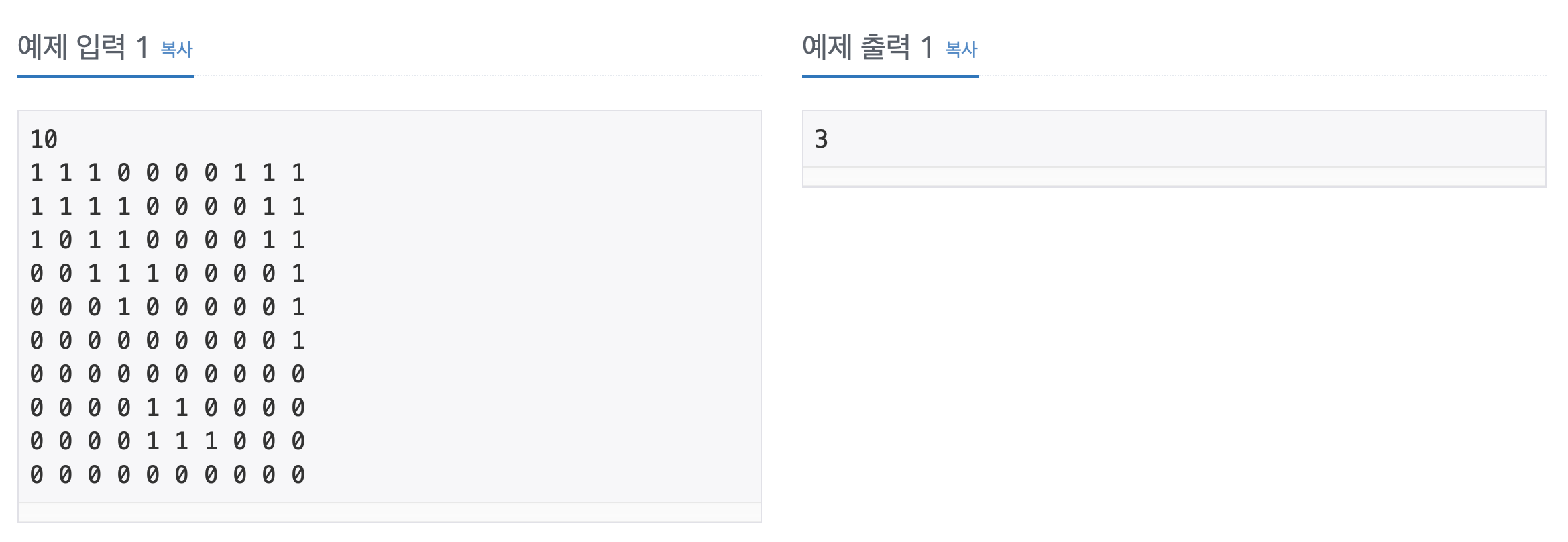
첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.
출력
첫째 줄에 가장 짧은 다리의 길이를 출력한다.
풀이

나는 이 문제를 좀 많이 특이하게 풀었다. 사실 n<=100이니까 시간초과가 없었지.. 그보다 컸으면 아휴..
우선 초기 상태의 map은 모든 섬이 1로 표현되어 있어서 섬끼리 구분이 되지 않는다. 따라서 bfs알고리즘을 이용해 각각의 섬의 숫자를 2이상의 값으로 map에 넣어줘 각각의 섬이 구별될 수 있도록한다.
그런뒤 다리의 최단 길이를 찾는 알고리즘을 시작한다. (사실 n값이 100 이하라서 그냥 무식한 방법을 써도 되겠구나 하고 풀었다.)
1) 우선 map을 탐색하면서 바다(0)이면서 상하좌우는 섬이 있는 지점을 찾는다.
2) 그 지점에 대해서 bfs를 수행하여 다른 섬까지 가는 거리를 구한다. 이 때 다리의 출발섬과 도착섬을 구분하기 위해서 bfs함수 호출시에 바다가 인접하고 있는 섬의 map 값을 넘겨준다.
3) 바다(0)인 경우에 상하좌우에 하나의 섬이 아닌 여러개의 섬을 인접할 수 있기 때문에 이전에 bfs함수에 넘겨준 출발섬의 map 값이 지금 인접한 것으로 찾은 섬의 map과 다른 경우 이에 대해서도 bfs함수를 호출해준다.
4) 1~3을 모든 map에 대해서 반복하면서 다리 길이의 최솟값을 찾는다.
질문게시판을 보면 간척사업 이런얘기 하면서 푸시던데.. 그 방식은 미래의 내가 시도하도록...맡깁니다...
#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
int map[101][101];
int visited[101][101];
int X[4] = {1, -1, 0, 0};
int Y[4] = {0, 0, 1, -1};
queue<pair<int, int>> island; //x, y
queue<pair<pair<int, int>, int>> check; //x, y, cnt
void island_bfs(int n, int x, int y);
int bfs(int n, int x, int y, int is);
int is_num = 1;
int b_min = 10000;
int main(void){
int n;
int n_x, n_y;
int near;
int cnt;
scanf("%d", &n);
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
scanf("%d", &map[i][j]);
}
}
for(int i=0; i<n; i++){ //섬들 구분
for(int j=0; j<n; j++){
if(map[i][j] == 1){
is_num++;
island_bfs(n, i, j);
}
}
}
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
if(map[i][j] == 0){
near = 0;
for(int k=0; k<4; k++){
n_x = i + X[k];
n_y = j + Y[k];
if(n_x < 0 || n_x >= n || n_y < 0 || n_y >= n)
continue;
if(map[n_x][n_y]!=near && map[n_x][n_y]!=0){
near = map[n_x][n_y];
cnt = bfs(n, i, j, near);
fill_n(&visited[0][0],101*101,0);
if(cnt < b_min)
b_min = cnt;
}
}
}
}
}
printf("%d\n", b_min);
}
void island_bfs(int n, int x, int y){
int p_x, p_y, n_x, n_y;
island.push(make_pair(x, y));
map[x][y] = is_num;
while(!island.empty()){
p_x = island.front().first;
p_y = island.front().second;
island.pop();
for(int i=0; i<4; i++){
n_x = p_x + X[i];
n_y = p_y + Y[i];
if(n_x < 0 || n_x >= n || n_y < 0 || n_y >= n)
continue;
if(map[n_x][n_y] == 1){
map[n_x][n_y] = is_num;
island.push(make_pair(n_x, n_y));
}
}
}
}
int bfs(int n, int x, int y, int is){
int p_x, p_y, n_x, n_y;
int cnt;
int result=10000;
check.push(make_pair(make_pair(x, y), 0));
visited[x][y] = 1;
while(!check.empty()){
p_x = check.front().first.first;
p_y = check.front().first.second;
cnt = check.front().second;
check.pop();
if(map[p_x][p_y]!=0 && map[p_x][p_y] != is){
while(!check.empty())
check.pop();
result = cnt;
break;
}
for(int i=0; i<4; i++){
n_x = p_x + X[i];
n_y = p_y + Y[i];
if(n_x < 0 || n_x >= n || n_y < 0 || n_y >= n)
continue;
if(map[n_x][n_y] != is && visited[n_x][n_y] == 0){
check.push(make_pair(make_pair(n_x, n_y), cnt+1));
visited[n_x][n_y] = 1;
}
}
}
return result;
}
'알고리즘 > PS - 백준' 카테고리의 다른 글
| [백준 1699 - C++] 제곱수의 합 : DP (0) | 2021.04.30 |
|---|---|
| [백준 9095 - C++] 1, 2, 3 더하기 : DP (0) | 2021.04.30 |
| [백준 2206 - C++] 벽 부수고 이동하기 : BFS (0) | 2021.04.12 |
| [백준 2638 - C++] 치즈 : BFS (0) | 2021.04.11 |
| [백준 2251 - C++] 물통 : BFS (0) | 2021.04.11 |