18352번: 특정 거리의 도시 찾기
첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개
www.acmicpc.net
문제
어떤 나라에는 1번부터 N번까지의 도시와 M개의 단방향 도로가 존재한다. 모든 도로의 거리는 1이다.
이 때 특정한 도시 X로부터 출발하여 도달할 수 있는 모든 도시 중에서, 최단 거리가 정확히 K인 모든 도시들의 번호를 출력하는 프로그램을 작성하시오. 또한 출발 도시 X에서 출발 도시 X로 가는 최단 거리는 항상 0이라고 가정한다.
예를 들어 N=4, K=2, X=1일 때 다음과 같이 그래프가 구성되어 있다고 가정하자.

이 때 1번 도시에서 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 2인 도시는 4번 도시 뿐이다. 2번과 3번 도시의 경우, 최단 거리가 1이기 때문에 출력하지 않는다.
입력
첫째 줄에 도시의 개수 N, 도로의 개수 M, 거리 정보 K, 출발 도시의 번호 X가 주어진다. (2 ≤ N ≤ 300,000, 1 ≤ M ≤ 1,000,000, 1 ≤ K ≤ 300,000, 1 ≤ X ≤ N) 둘째 줄부터 M개의 줄에 걸쳐서 두 개의 자연수 A, B가 공백을 기준으로 구분되어 주어진다. 이는 A번 도시에서 B번 도시로 이동하는 단방향 도로가 존재한다는 의미다. (1 ≤ A, B ≤ N) 단, A와 B는 서로 다른 자연수이다.
출력
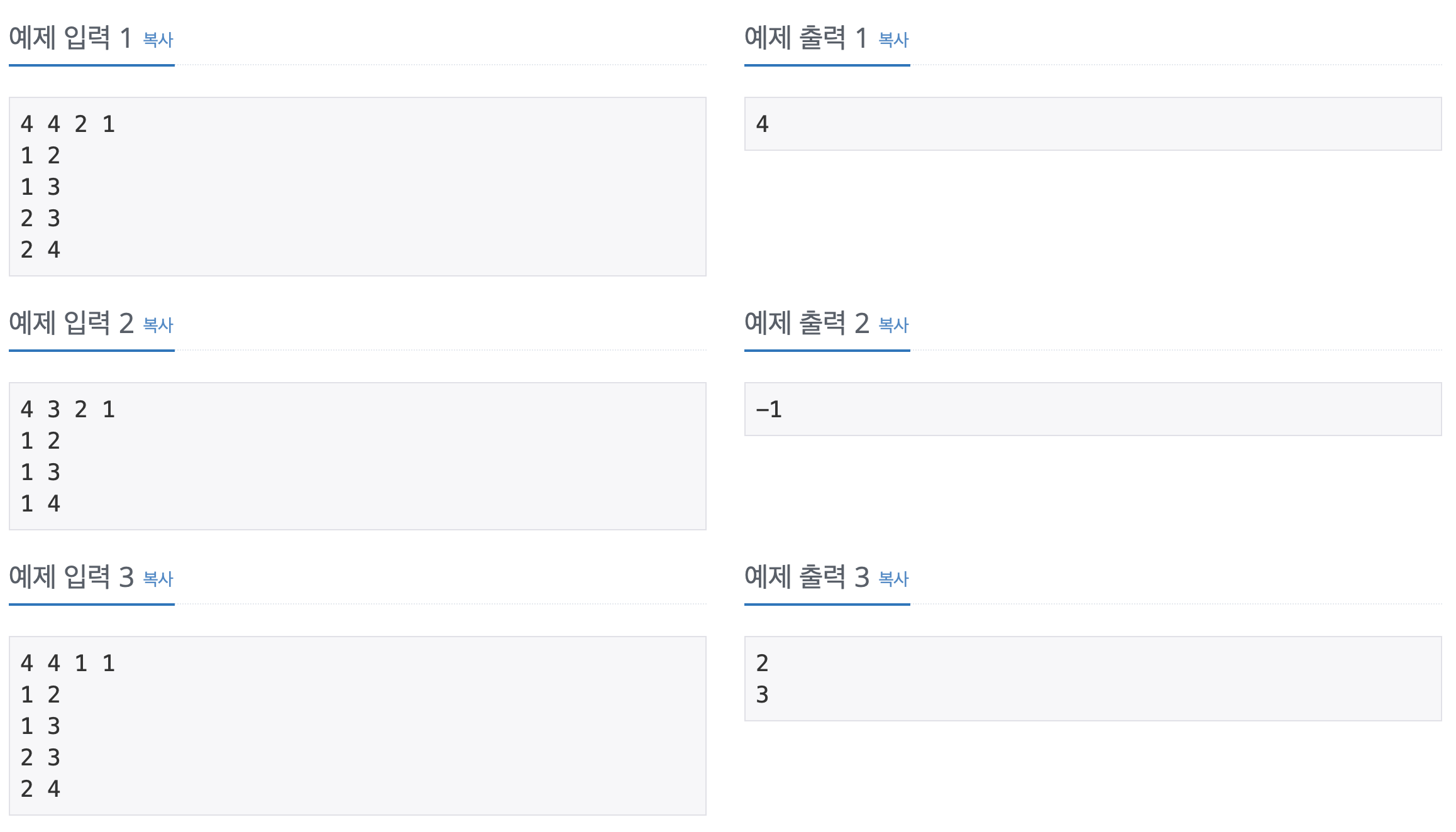
X로부터 출발하여 도달할 수 있는 도시 중에서, 최단 거리가 K인 모든 도시의 번호를 한 줄에 하나씩 오름차순으로 출력한다.
이 때 도달할 수 있는 도시 중에서, 최단 거리가 K인 도시가 하나도 존재하지 않으면 -1을 출력한다.
풀이
이 문제에선 최대 도시수가 300,000로 매우 크다. 따라서 길이 있음을 표시하는데에 300,001 * 300,001 크기의 정적인 2차원 배열을 사용할 수 없다. 따라서 벡터를 사용하여 연결된 길을 저장하였다. 이 문제에선 길이 단방향이기때문에 이렇게 저장하여도 상관없는것이다.
또한 STL에 제공되는 priority_queue를 사용하여 다익스트라 알고리즘을 구현하였다.
(다익스트라 알고리즘 관련 내용은 excited-hyun.tistory.com/23 참고)
길의 cost는 모두 1로 동일하므로 각각의 길의 cost를 저장해둘 필요는 없다.
#include <cstdio>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int dist[300001];
vector< vector<int> > way;
int main(void){
int n, m, k, x;
int city_a, city_b;
int here, cost;
int there, nextCost;
int cnt =0;
priority_queue<pair<int ,int>> pq;
scanf("%d %d %d %d", &n, &m, &k, &x);
way.resize(n+1);
for(int i=0; i<m; i++){
scanf("%d %d", &city_a, &city_b);
way[city_a].push_back(city_b);
}
for(int i=1; i<=n; i++){
dist[i] = n;
}
dist[x] = 0;
pq.push(make_pair(0, x));
while(!pq.empty()){
cost = -1 * pq.top().first;
here = pq.top().second;
pq.pop();
if(dist[here] < cost)
continue;
for(int i=0; i<way[here].size(); i++){
there = way[here][i];
nextCost = cost + 1;
if(nextCost < dist[there]){
dist[there] = nextCost;
pq.push(make_pair(-nextCost, there));
}
}
}
for(int i=1; i<=n; i++){
if(dist[i] == k){
printf("%d\n", i);
cnt++;
}
}
if(cnt == 0){
printf("-1\n");
}
}
'알고리즘 > PS - 백준' 카테고리의 다른 글
| [백준 1916 - C++] 최소비용 구하기 : 다익스트라(Dijkstra) (0) | 2021.02.01 |
|---|---|
| [백준 1753 - C++] 최단경로 : 다익스트라(Dijkstra) (0) | 2021.02.01 |
| [백준 5014 - C++] 스타트링크 : BFS (0) | 2021.01.30 |
| [백준 1012 - C++] 유기농 배추 : BFS (0) | 2021.01.30 |
| [백준 2660 - C++] 회장뽑기 : BFS (0) | 2021.01.29 |